2009년05월23일 20번
[과목 구분 없음] 그림과 같이 a, b, c 3개의 각을 관측하였다. 오차를 보정한 각 a와 각 c의 조정각은? (단, a=35° 12′20″, b=30° 10′10″, c=65° 22′45″이다)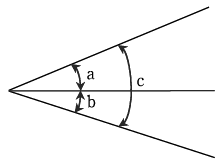

- ① (a) 35˚ 12′15″, (c) 65˚ 22′40″
- ② (a) 35˚ 12′15″, (c) 65˚ 22′50″
- ③ (a) 35˚ 12′25″, (c) 65˚ 22′40″
- ④ (a) 35˚ 12′25″, (c) 65˚ 22′50″
(정답률: 77%)
문제 해설
먼저, 보정각은 실제 각도에서 오차를 보정한 값이므로, a와 c의 보정각은 각각 35˚ 12′20″에서 오차를 보정한 값이다.
다음으로, 오차를 보정하기 위해서는 b의 각도를 이용해 삼각함수를 이용해야 한다.
먼저, 삼각형 ABC에서 각 B의 크기는 180˚ - (a + c) = 79˚ 27′ 35″이다.
이제, 삼각형 ABC에서 각 A와 각 C의 보정각을 구하기 위해 코사인 법칙을 이용하면 다음과 같다.
cos(a 보정각) = (b^2 + c^2 - a^2) / 2bc
cos(c 보정각) = (a^2 + b^2 - c^2) / 2ab
여기서, a, b, c는 각각 원래의 각도이다.
따라서, a 보정각은 cos^-1((b^2 + c^2 - a^2) / 2bc) = 35˚ 12′ 25″이고, c 보정각은 cos^-1((a^2 + b^2 - c^2) / 2ab) = 65˚ 22′ 40″이다.
따라서, 정답은 "(a) 35˚ 12′25″, (c) 65˚ 22′40″"이다.
다음으로, 오차를 보정하기 위해서는 b의 각도를 이용해 삼각함수를 이용해야 한다.
먼저, 삼각형 ABC에서 각 B의 크기는 180˚ - (a + c) = 79˚ 27′ 35″이다.
이제, 삼각형 ABC에서 각 A와 각 C의 보정각을 구하기 위해 코사인 법칙을 이용하면 다음과 같다.
cos(a 보정각) = (b^2 + c^2 - a^2) / 2bc
cos(c 보정각) = (a^2 + b^2 - c^2) / 2ab
여기서, a, b, c는 각각 원래의 각도이다.
따라서, a 보정각은 cos^-1((b^2 + c^2 - a^2) / 2bc) = 35˚ 12′ 25″이고, c 보정각은 cos^-1((a^2 + b^2 - c^2) / 2ab) = 65˚ 22′ 40″이다.
따라서, 정답은 "(a) 35˚ 12′25″, (c) 65˚ 22′40″"이다.
이전 문제
다음 문제



